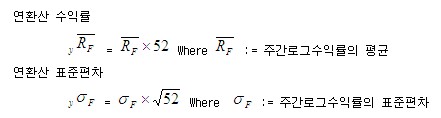728x90

Downside Deviation

현대 포트폴리오이론에 의하면 포트폴리오의 위험은 투자수익률의 변동성으로 정의하고 있으며 대표적으로 표준편차가 변동성을 측정하는 지표로 쓰이고 있다. 그러나 까놓고 얘기하자면 수익률이 좋아져서 매일 10%이상씩 버는 펀드에게 "표준편차가 커져 넌 위험한 펀드니까 추천할 수 없어~"라고 말하기엔 뭐하다.


사실 수익률이 위로 변동하는것은 위험이 아니고 아래로 변동하는 것만이 위험이라고 하는 것이 보다 자연스럽다. 이런 사고방식에 따른 위험을 다운사이드 위험 (Downside risk)라 한다. Downside Deviation은 기준이 되는 수익률보다 낮은 수익률에 대해서만 변동성을 구한 것이다.

Monthly Downside Deviation = The Square Root of (the Sum of ((Monthly ROR - Monthly MAR) squared))) / (Number of Data points)
where MAR is Minimum Acceptable Rate of Return

참고로 Quantlib의 엑셀버전인 QuantlibXL은 qlDownsideDeviation()함수를 지원한다. 계산하려고 따로 만들 필요는 없다.

출처 : http://timebird.egloos.com/2161019
저작자표시

'주식 > 펀드' 카테고리의 다른 글

베타지수와 샤프지수  (0) 2009.03.25
수익률 계산 및 위험지표  (0) 2009.03.25
펀드의 위험 지표 보는 법  (0) 2009.03.24
트래킹 에러 (tracking error : 추적 오차)  (0) 2009.03.24
펀드 위험 분석  (0) 2009.03.24
728x90
샤프지수[Sharpe Ratio]

특정 펀드가 한 단위의 위험자산에 투자해서 얻은 초과수익의 정도를 나타내는 지표이다. 샤프척도(Sharpe measure)라고도 하며, 트레이너지수(Treynor ratio)·젠센지수(Jensen's ratio)와 함께 위험을 감안하여 펀드를 측정하는 방법으로, 두 지수와 더불어 위험조정 후 수익률지수로 통칭된다.

 

1990년 노벨경제학상을 받은 미국의 윌리엄 샤프(William F.Sharpe)가 1954년부터 1963년까지 34개 펀드의 실적을 분석하여 개발하였다.

 

트레이너지수가 펀드의 베타계수만을 고려하는 반면 전체위험을 고려하는 표준편차를 사용하고, 최소 1개월 이상의 수익률 데이터를 필요로 한다. 분산투자가 잘 되어 있지 않은 펀드를 평가할 때 유용한 방법으로, 값이 높을수록 펀드의 수익률이 우수하다는 것을 보여준다.

 

 베타지수[Beta]

시장전체에 대한 펀드수익률의 민감도를 말함. 해당펀드의 수익률을 종합주가지수로 나눈 값으로, 베타지수가 1보다 크면 주가지수 변동률보다 펀드의 수익률 변동이 크다는 것을 의미하며, 1보다 작으면 주가지수 변동률보다 펀드의 수익률 변동이 작다는 것을 의미한다.

 

베타가 1.0 이라면 시장수익률과 동일한 민감도를 가지며, 만일 0.5나 0.8처럼 1.0보다 작다면 시장수익률보다 둔감하게 움직임(안정적인 포트폴리오), 1.0보다 크다면 시장수익률보다 민감하게 움직임(위험이 큼)으로 볼 수 있습니다. 베타의 경우 펀드 수익률로 계산되기 때문에 편입비를 감안하여 보셔야 합니다.

베타값이 1보다 크다는 것은 시장상승시 더 많이 상승할 수 있지만,

하락시에는 더 많이 하락한다는 것을 말합니다.

샤프지수는 포트폴리오 1단위 위험에 대한 초과수익 정도를 나타내는 지표로 (펀드 주간 로그수익률 평균 - 무위험이자율 주간로그수익률 평균)/펀드 주간로그수익률의 표준편차로 계산합니다.

 

당사에서는 현재 무위험이자율로 CD를 사용 중으로 회사마다, 기관마다 샤프지수를 적용하는 기준은 상이합니다. 아울러 동일유형이 아닌 다른 유형의 샤프지수를 상호비교하는 것은 대단히 위험한 발상입니다. 샤프지수는 동일한 유형에 대해서 동일한 기준으로 적용할 경우 상호 비교하는 것이 의미가 있습니다.

물론 샤프지수가 크다는 것은 무위험이자율대비 초과수익 정도가 크다는 것으로 설명될 수 있지만, 무위험이자율대비 성과가 저조하거나, (-)수익률시 설명력이 떨어지는 문제가 있습니다. 이에 따라 음의 경우 수정샤프지수를 위험지표로 사용하기도 합니다.

개인적으로는 주식형의 경우 편입비를 감안한 베타지수를 선호합니다. 샤프지수는 상호비교하기 위한 지표로 좋은 지표가 될 수 있지만, 실제 시장과 비교하기는 어려운 면이 있습니다.

 출처 : http://hobbangoo.tistory.com/archive/200901


'주식 > 펀드' 카테고리의 다른 글

Downside Deviation  (0) 2010.12.01
수익률 계산 및 위험지표  (0) 2009.03.25
펀드의 위험 지표 보는 법  (0) 2009.03.24
트래킹 에러 (tracking error : 추적 오차)  (0) 2009.03.24
펀드 위험 분석  (0) 2009.03.24
728x90
1) 평균수익률(Average Return)
펀드의 기간별 수익률 평균을 의미하며 제로인에서는 주간수익률을 기준으로 1개월, 3개월, 6개월, 9개월, 12개월, 18개월, 24개월, 36개월, 60개월 동안 주간수익률의 평균을 계산합니다. 다만 계산의 편의를 위하여, 1개월은 4주, 3개월을 13주, 6개월은 26주, 1년은 52주를 사용합니다.
[참고]
제로인은 평균수익률 및 위험지표들을 계산하기 위해 주 최초 영업기준가(전주말 운용종가)와 직전 주 최초 영업기준가(직전주말 운용종가)를 이용해 산출한 "주간 수익률"을 사용합니다. 다만 표시되는 기간을 고려, 주간수익률을 해당 기간으로 환산하거나 연환산(Annualized)해서 사용하고 있습니다. 이는 단순실현수익률과 위험지표들을 쉽게 비교할 수 있도록 하기 위해서입니다. 또한, 무위험수익률로는 CD91일물의 수익률을 사용하고 있습니다.

2) 표준편차(Standard Deviation)
투자기간 동안 펀드수익률이 평균수익률과 대비하여 변동한 범위를 측정하기 위한 통계량으로써, 펀드의 위험 정도를 나타내는 지표로 이용되고 있습니다. 값이 클수록 변동성이 심하므로 위험이 크고, 값이 작을수록 위험이 작다고 할 수 있습니다.

3) 베타(Beta)
시장변화에 대한 펀드수익률의 민감도를 나태내기 위해서 베타를 사용하며, KOSPI200지수를 시장으로 간주하고 있습니다. 베타의 크기에 따른 의미는 다음과 같습니다.
즉, 시장수익률과 펀드수익률과의 상호변동관계를 나타내는 지표로 사용되는 베타는 KOSPI가 1% 변할 때 펀드수익률이 몇 % 변하는지를 나타냅니다. 베타계수가 1인 펀드는 종합주가지수와 평균적으로 동일한 방향으로 동일한 비율만큼 움직인다는 것을 의미 합니다. 예를 들어, 베타계수가 1.5인 펀드는 시장수익률이 1%증가(감소)할 때 같은 방향으로 평균적으로 약 1.5% 증가(감소)한다고 할 수 있습니다.

4) 결정계수(R2: R-square)
종속변수의 분산 중 독립변수(또는 설명변수)에 의해 설명되는 분산의 비율을 의미하는 통계적인 용어로, 0에서 1까지의 값을 갖습니다.(백분율로 표시할 수도 있습니다.) 결정계수가 1이라는것은 독립변수(Ex : 시장수익률)가 종속 변수(Ex : 펀드수익률)의 움직임을 완전하게 설명한다는 것을 의미합니다.

결정계수는 단일요인 모형인 시장모형(Market Model)을 이용하여 개별주식이나 펀드의 수익률을 주가지수에 대해 회귀분석하는 경우 기울기를 나타내는 베타 값의 정확성을 표시하는 보조지표로 이용될 수 있습니다. 회귀식의 기울기(베타)가 1이고 결정계수가 0.3이라면 주가지수가 개별 주식이나 펀드의 수익률을 30% 정도 설명하는 것으로 볼 수 있습니다. 즉, 베타계수에 대한 신뢰도가 약 30% 정도 되는 것으로 이해할 수 있습니다.

가장 간단하면서 많이 사용하는 시장모형에서는 설명변수가 시장수익률밖에 없으므로, 이 모형에서 결정계수는 포트폴리오가 가지는 전체 분산(위험)중 시장수익률이 설명하는 비중을 의미합니다. 따라서 시장모형에서의 결정계수는 포트폴리오의 위험 중 시장위험과 관련된 정도를 나타냅니다.

포트폴리오 총위험(분산) = 시장위험(분산) + 포트폴리오 고유위험(분산)
시장모형에서의 결정계수는 다음과 같이 나타낼 수 있습니다.

5) 트래킹 에러(TE: Tracking Error)
트래킹 에러는 일반적으로 일정기간 투자한 펀드의 수익률이 이에 대응하는 지수 수익률에 비해 어느 정도의 차이를 보이는가를 측정하는 지표로 (지수)추적오차라고도 합니다. 펀드평가에서는 펀드의 기간수익률과 이에 대응하는 벤치마크 지표 수익률과의 차이에 대한 변동성을 의미합니다.

실제 자료에서 트래킹 에러는 일정기간 펀드의 초과수익률(Excess Return)에 대한 표준편차로 측정하며, 제로인은다음의 식으로 트래킹 에러를 계산합니다.
이때 TE는 펀드의 총위험(표준편차)이 커질수록 또한 결정계수가 작아질수록 커지게 됩니다. 또한, 펀드의 총위험은 주식의 편입비에 비례하여 커지는 경향을 보이므로, 주식편입비도 간접적으로 TE에 영향을 미치게 됩니다.


6) 샤프지수(Sharpe Ratio)
펀드의 위험 1단위에 대한 초과수익의 정도를 나타내는 지표입니다. 다시 말해서, 1이라는 위험을 부담하는 대신 얻은 대가, 즉 초과수익이 얼마인가를 측정하는 지표입니다. 따라서 샤프지수가 높을수록 투자성과가 성공적이라고 할 수 있습니다.
무위험 초과수익률 (즉, 수익률에서 무위험 수익률을 뺀 수익률)을 사용하는 이유는 위험을 부담함으로써 얻어지는 수익에서 의미있는 것은 무위험자산(전혀 위험을 부담하지 않는 자산)에 투자해서 얻는 수익을 초과하는 것뿐이기 때문입니다.


7) 수정샤프지수(Modified Sharpe Ratio)
샤프 지수의 경우, 펀드의 초과 수익률이 음의 값을 가지는 경우에는 해석할 수 없다는 문제를 가지고 있습니다. 즉, 다른 조건이 동일한 경우 수익률은 높을수록 그리고 위험은 낮을수록 좋은 성과를 나타내는 것으로 나타나야 하는데, 초과수익률이 음의 값을 가지는 경우에는 오히려 반대로 나타납니다.

이런 문제를 보완하기 위한 지표로서 초과수익률이 (+)인 경우 샤프지수와 같은 값을 갖게 되고 반대로 (-)인 경우 수익률은 높을수록 그리고 위험은 낮을수록 좋은 성과를 나타내기위해 초과수익률에 표준편차를 곱한 값을 사용합니다.


8) 트레이너 지수(Treynor Ratio)
펀드의 체계적 위험 1단위당 무위험 초과수익률을 나타내는 지표입니다. Sharpe는 무위험 초과수익에 기여하는 펀드의 위험으로 총위험인 표준편차를 사용한 반면, Treynor는 분산투자가 가능한 경우, 비체계적 위험은 투자수익에 기여할 수 없으며 체계적 위험만이 초과수익에 기여한다는 관점에서 펀드의 위험으로 체계적 위험인 베타()를 사용합니다.


9) 젠센의 알파(Jensen's Alpha)
펀드의 수익률이 균형상태에서의 수익률보다 얼마나 높은지를 나타내는 지표입니다. 다시 말해, 펀드 수익률에서 적정(or 기대)수익률을 뺀 값을 의미합니다. 따라서, Jensen's Alpha가 클수록 성공적인 투자 성과를 나타내는 것입니다.
위 식을 보면 Jensen's Alpha란 펀드가 취한 위험(=베타) 하에서 요구되는 기대수익률을 얼마나 초과했는가를 나타내는 것임을 알 수 있습니다.


10) 정보비율(IR : Information Ratio)
적극적인 투자활동의 결과 나타나는 초과수익률과 적극적인 활동에 따른 수익률의 표준편차의 비율을 말하는데, Reward-to-Variability Ratio(RVR)라고 부르기도 합니다. 이 비율이 높을수록 더 좋은 투자활동으로 판단합니다. 펀드의 벤치마크를 가정하는 경우 IR은 다음과 같이 표시됩니다.


11) 효용함수에 의한 확실성 등가(CE : Certainty Equivalence)
샤프 지수, 트레이너 지수 등은 각각의 장점에도 불구하고 펀드의 초과 수익률이 음의 값을 가지는 경우에는 해석할 수 없다는 문제를 가지고 있습니다. 즉, 다른 조건이 동일한 경우수익률은 높을수록 그리고 위험은 낮을수록 좋은 성과를 나타내는 것으로 나타나야 하는데, 이들 지표들은 초과수익률이 음의 값을 가지는 경우에는 오히려 반대로 나타납니다.

이러한 문제점을 해소할 수 있는 지표로 수익률과 위험의 관계를 나타내는 효용함수를 이용한 효용값(확실성 등가, 위험이 전혀 없는 수익률)을 사용할 수 있습니다. 투자자의 기본적인 특성(위험회피형)을 만족시키면서 가장 간단하게 사용할 수 있는 효용함수는 다음과 같은 위험과 기대수익의 선형함수로 표현할 수 있습니다.
출처 : http://www.funddoctor.co.kr/html/method/method.jsp

'주식 > 펀드' 카테고리의 다른 글

Downside Deviation  (0) 2010.12.01
베타지수와 샤프지수  (0) 2009.03.25
펀드의 위험 지표 보는 법  (0) 2009.03.24
트래킹 에러 (tracking error : 추적 오차)  (0) 2009.03.24
펀드 위험 분석  (0) 2009.03.24

+ Recent posts

티스토리툴바